Every year my girlfriend and her friends organize their own twist of Secret Santa, but the overall rules are pretty standard. Recently, she was telling me about some recurring problem in the game: sometimes, non-trivial subsets of players end up ‘closed’ within themselves. Therefore, the original set of players gets partitioned, which breaks the natural flow of gift exchange between them. She said that they use a website that assigns a particular person to each one and then sends individual results for the respective e-mail addresses. However, it was clear that the service does not account for the undesired partitioning. So, she asked:

How could we generate the assignments and prevent this issue from happening?

We discussed for a few minutes and already came up with a simple algorithm that (intuitively) seemed to work. It was almost certain that such procedure would give us solutions that suited needs, but I was wondering about the generality of those solutions. So, I went out to prove it. In what follows, the real-world problem mentioned will be modeled and described in the language of graph theory. After our main result, an algorithm to generate solutions in a constructively manner will be provided.

Laying out the concepts

After the name drawing phase, the general configuration for the players and their relations can be represented as a directed graph, where nodes correspond to the participants and directed edges (or arcs) describe the “assignment” between pairs of players. Here, I’m going to establish a particular interpretation that I believe it’s easily readable when looking at the diagrams. For instance, the graph

reads “Bob was assigned to Alice” or, more explicitly, “Alice will hand out her gift to Bob”. So, the direction of the edges simply maps to the gift exchange process. We may now present the graph structure that defines a valid setting for the Secret Santa game.

Definition. Let $G = (V, A)$ be a directed graph, where $V$ is the set of vertices and $A$ is the set of arcs. The digraph $G$ is said to be a Secret Santa setting if it satisfies the following:

  (i) $\textrm{deg}^{-}(v) = \textrm{deg}^{+}(v) = 1$, $\forall \hspace{1pt} v \in V$;

  (ii) $\nexists \, (v, v) \in A$, $\forall \hspace{1pt} v \in V$.

A quick comment about notation: given a node $v$, $\textrm{deg}^{-}(v)$ denotes the indegree of $v$, while $\textrm{deg}^{+}(v)$ indicate its outdegree. Moreover, given any two nodes, $v$ and $u$, the tuple $(v, u)$ is an ordered pair that represents an arc going from $v$ to $u$.

The first property just says that, for each vertex, only a single arc enters and a single arc leaves. This ensures that each person will be assigned to only one player and also that there will be a single assignment for each player. The second condition states that no individual is self-assigned.

Let us show some examples of Secret Santa setting graphs:

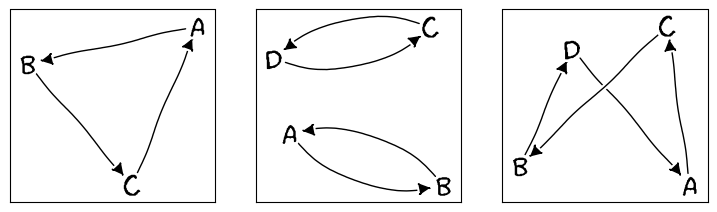
Now, if we recall the starting point of this discussion, it is clear that the issue itself just alludes to the fact that the Secret Santa setting can display cases which are actually a disjoint union of graphs. For instance, look at the second graph in the examples above.

So, the problem here is about connectivity. A desirable solution is then to develop some way of constructing Secret Santa setting graphs that are also connected.

Gift exchange is a circle of joy: a proof

As I wrote earlier, something got me curious about the general structure of digraphs that satisfy the laid out constraints. It is not something difficult to conceive and conjecture upon, however, a proof was still lacking. Eventually, I came up with an idea that worked. Although simple, and maybe trivial to some that may read this, I thought it was worth sharing, so, this section is dedicated to such result.

Lemma. Let $G$ be a connected Secret Santa setting graph with $N$ nodes. Then $G$ is the directed cycle graph $C_{N}$.

Proof. Consider the case where $N=2$. It is clear that the only possible Secret Santa setting is $C_{2}$. Actually, it’s not hard to see that the same goes for $N=3$. Given our base cases, we can do induction on the number of nodes.

Assume the lemma is valid for some $N \in \mathbb{N}$, i.e. we have the directed cycle graph $C_{N}$ as the only possible structure for a connected Secret Santa setting with $N$ nodes. Now, suppose we want to add another node $w$ to it, while trying to satisfy the hypothesis conditions. In order to introduce this new vertex to the graph, we need to take two different nodes $v, u \in C_{N}$ and connect them directly to $w$; more explicitly, to guarantee that $\textrm{deg}^{-}(w) = \textrm{deg}^{+}(w) = 1$ then a new pair of arcs must be created. Without loss of generality, suppose we just construct the arcs $(v, w)$ and $(w, u)$. Of course, there is a problem: since $v$ and $u$ were already part of $C_{N}$, these new arcs imply that $\textrm{deg}^{+}(v) = 2$ and $\textrm{deg}^{-}(u) = 2$. There are two scenarios here:

  A. Nodes $v$ and $u$ are $k > 1$ arcs apart.

In this case, trying to make the digraph a Secret Santa setting again would require to remove the original arc that started at $v$, keeping only the new arc $(v,w)$, and to also remove the original arc arriving at $u$, keeping our recent $(w,u)$. However, this would make our graph disconnected, as there were nodes between $v$ and $u$ that got separated from the original cycle. Hence, it is not possible to achieve such goal here.

  B. Nodes $v$ and $u$ are adjacent.

In this case, it is possible, since one can simply erase the arc $(v, u)$. Now, the digraph remains connected and every vertex satisfy the conditions of a Secret Santa setting. Moreover, it’s clear that our changes to the original graph transformed it into the cycle $C_{N+1}$. In summary,

\[\left( C_{N} \cup \lbrace w, (v, w), (w, u) \rbrace \right) \setminus \lbrace (v, u) \rbrace = C_{N+1} \, ,\]

which concludes our proof. $\,\blacksquare$

Finally, we now know that, by imposing all desirable properties, the solution will always be a cycle digraph whose size is determined by the number of participants.

An algorithm for setting up the game

Here, we will end by discussing about an algorithm that can be used to create assignments between players in such a way that it encompasses the concepts we’ve presented so far and, consequently, solves the original issue that led to all of this. The first option would be to start with the data structure that represents a generic digraph, but only containing the nodes. Then, one would create all arcs randomly, one by one, while employing conditions to guarantee that our constraints are being satisfied. However, this would be better if we didn’t knew about the previous lemma. Now, for any given number of vertices, we already know that there is only a single digraph structure that suits our needs: a cycle. Therefore, we simply need a data structure that can describe such fundamental relations, which can be done with something as simple as an array, and then we just have to randomly set ‘labels’ to each one of our nodes. For instance, consider the following pseudocode:

algorithm secret-santa is
    input: participants array P := [p1, p2, ..., pN],
           where p_j denotes the j-th player
    output: array A containing tuples that correspond 
            to arcs between players
    
    rndP := shuffle(P)
    C := append(rndP, rndP[0])

    A := [ ]
    
    for each i from 0 to length(P) do
        A := append(A, tuple(C[i], C[i+1]))

    return A

There you go, as simple as that. By taking the time of going out to prove something that was only an intuition, it provided us with a nice result that can be used to build a simpler algorithm, considering the alternative of procedurally creating the graph using some other data structure that could be more complex and, more than that, having to explicitly perform operations to check if constraints are being met during the process.